In the previous post, from a cluster of touching mouse chromosomes:
points belonging to negatively curved domains of a contour can be isolated :
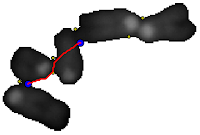
the path (red) between the two points can be determined by minimizing the "greyscale cost", that is through the valleys between the two points is the image is viewed as a landscape.
All the paths can be determined (blue):Those paths in blue were obtained from the previous binary image:
The paths were sorted according to their cost :
The four paths with the smallest cost are figured in red, they are "inside" the cluster. Some paths are partially "outside" the cluster and thus are not geodesic routes inside the cluster.
Now if paths are calculated from a 8 bits greyscale image where the background was set to 255 (a naïve idea supposed to prevent a path to go "outside" a cluster):
some routes between two points, go along the contour. The two first routes to with the smallest costs do correspond to touching domains between the chromosomes. However when routes with higher cost are selected:
some correspond to the cluster contour and not to contact domains between the chromosomes, because the cost (sum of pixels grey value) along the contour is probably lower than the cost of a shorter path which have to climb over a contact domain between two chromosomes.
Additional features may distinguish routes belonging to contour from those providing solution to separate chromosomes:
Minimal cost routes are still better to separate chromosomes than routes obtained with euclidian distance:
Download code
 |
| DAPI stained mouse chromosomes |
To separate the chromosomes, it is tempting to cut between the closest pairs of points.
Python provides itertools.combinations(); the closest pairs of points are in the set of the combinations of every pairs of points:
Each line
shows the euclidian distance between two points, the four shortest lines
correspond more or less to the contact domains between the chromosomes,
cuting along them provides a way to separate the chromosomes.
It
should be possible to do better by using a geodesic distance between
the points, that is using a path inside the cluster of chromosomes. In
the following example: two paths
(depending on the chosen pixel neighborhood) between the two blue points
were overlaid on a binary image (background is set to 255 and the
foreground to 0).
the cluster contourthe cluster contour
The path were determined as follow using skimage 0.8dev:
graph.route_through_array(negbin ,p1,p2,fully_connected=False)
or
graph.route_through_array(negbin ,p1,p2,fully_connected=True)
with negbin, the negative binary image and p1, p2 the two points figured in blue.
If the
background (0) is set to 255 (white) in the grey scale image:
the path (red) between the two points can be determined by minimizing the "greyscale cost", that is through the valleys between the two points is the image is viewed as a landscape.
 |
The paths were sorted according to their cost :
The four paths with the smallest cost are figured in red, they are "inside" the cluster. Some paths are partially "outside" the cluster and thus are not geodesic routes inside the cluster.
Now if paths are calculated from a 8 bits greyscale image where the background was set to 255 (a naïve idea supposed to prevent a path to go "outside" a cluster):
some routes between two points, go along the contour. The two first routes to with the smallest costs do correspond to touching domains between the chromosomes. However when routes with higher cost are selected:
some correspond to the cluster contour and not to contact domains between the chromosomes, because the cost (sum of pixels grey value) along the contour is probably lower than the cost of a shorter path which have to climb over a contact domain between two chromosomes.
 |
| red route on the right resolve touching chromosomes |
 |
| The shortest path (on the right) cuts inside the chromosome |
Download code