Selecting a maximal area quadrilateral from four random points

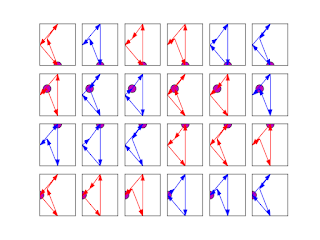
To calculate the area of a quadrilateral with the points coordinates, the points are supposed to be taken clockwise or counter clock wise.When the shoelace formula is applied on each of  4!=24 tuple of four points, different values can be obtained:

For example, the area of the square (on top left) with the points taken clock wise, is equal to 4. The 24 ways to calculate the area yield only two values 0 or 4. The quadrilateral of area equal to 0 is plotted on top right (red), this quadrilateral is self intersecting. The trapeze area (down left) is equal to 3, the 24 ways to calculate the area yied three values :0, 1, 3 and the maximal value of the area corresponds to a non intersecting quadrilateral (blue, down right).

Quadrilaterals were build from randomly chosen points, their area was calculated by taking the original points order:

Some of them are self intersecting (first, top left) or degenerated (the 10th). By searching the order of the points giving the maximal area, non self-intersecting quadrilaterals can be found:

If both initial and final quadrilaterals are overlayed:

Compare from the previous post, the function to calculate the area was modified http://people.virginia.edu/~ll2bf/docs/various/polyarea.html).

Play with the code on cloud.sagemath or download code.

Update (2014-04):

A quadrilateral of maximal area is found using brute force (by looking for the permutations of four points). Since cyclic or circular permutations of four points yield quadrilaterals with the same area, the search of maximal area should be performed not on a set of permutations of points but on a set of unique cyclic permutations of four points (a "necklace") possibly with Sawada's algorithm

Simple direct quadrilaterals found with the shoelace formula

The shoelace formula can computes the area of a quadrilateral  from the points coordinates . The formula requires that the points are taken clockwise or counter clockwise,  that is a quadrilateral must not be self crossing.
A criterion implemented in python was proposed to check if two segments are intersecting, which should be the case for a self-crossing quadrilateral.

With four points, there is  4!=24 ways to calculate the area. With points defining a square, according to the points order, the area takes three values: -2, 0 and 2 for indirect, self crossing and direct square:

The first point is the purple one.

The first square (top left in red) defined by the points (1, 0), (2, 1), (1, 2), (0, 1):

((1, 0), (2, 1), (1, 2), (0, 1)) False 2.0

is detected as non self crossing (False), and the shoelace formula gives an area equal to 2 as waited  for this direct square. There is a problem for some self crossing quadrilaterals:

((1, 0), (2, 1), (0, 1), (1, 2)) False 0.0
((1, 0), (1, 2), (2, 1), (0, 1)) True 0.0

The second quadrilateral is not detected as self crossing, however the shoelace formula yield an area equal to zero, as the third quadrilateral which is correctly dtected as self crossing (True). The last quadrilateral (blue one, down right):

((0, 1), (1, 2), (2, 1), (1, 0)) False -2.0

is correctly deteted as non self crossing (False) and indirect with a negative "area" equal to -2

Trying with points yielding non convex quadrilaterals yields six values -0.95,-0.65,  -0.4, 0.4, 0.65,  0.95. None is detected as self crossing:

With other points defining a possible convex quadrilateral:

Several values are found. The maximal area value : 1.465, corresponds to the four simple quadrilaterals (non self crossing):

((1.1, 0.3), (1.7, 1.4), (1, 2), (0, 1)) False 1.465

((1.7, 1.4), (1, 2), (0, 1), (1.1, 0.3)) False 1.465

((1, 2), (0, 1), (1.1, 0.3), (1.7, 1.4)) False 1.465

((0, 1), (1.1, 0.3), (1.7, 1.4), (1, 2)) False 1.465

It seems that the maximal area value found from the set of 24 possible quadrilaterals correspond to simple direct quadrilaterals, thus testing if the four points define a non self crossing quadrilateral may not be usefull.

January 3, 2013:
The script is modified so that the quadrilaterals are plotted with matplotlib.patches.Polygon:

Download code
Play with the code on cloud.sagemath.com